
Дело было в 1934 году, 82 года назад. Альберт Эйнштейн уже как 12 лет был лауреатом Нобелевской премии. В то время не было Вайберов, Телеграммов и Ватсапов, поэтому люди, живущие разных городах и странах писали письма на бумаге, шли на почту, клеили почтовые марки и отправляли их.
Именно таким образом переписывался Альберт Эйнштейн со своим другом Максом Вертгеймером. Тоже весьма известной личностью, отцом-основателем гештальтпсихологии, автором известной фразы: "Целое — есть нечто большое, чем сумма его частей".
И вот однажды Макс Вертгеймер решил подшутить над своим приятелем-физиком. Написал ему письмо и придумал очень оригинальную задачу, которую Эйнштейн наверняка оценил и посмеялся. Теперь ваша очередь.
Итак, у нас имеется холм. Симметричный идеальный холм. 1 миля вверх по склону и 1 миля вниз по склону. Автомобиль сначала въезжает на холм, а затем должен спуститься. Поднимается он со средней скоростью 15 миль в час. Вопрос: с какой скоростью должен спускаться автомобиль, чтобы средняя скорость на всем пути была 30 миль в час?
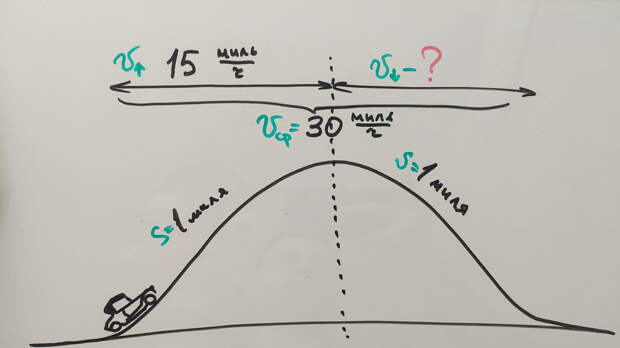
Ничего подозрительно сложного в задаче нет. Чтобы найти среднюю скорость, берем скорость движения вверх, скорость движения вниз и делим пополам, делов-то. Отсюда выражаем скорость спуска и получаем вполне логичные 45 миль в час. Вот только это неправильное решение и неправильный ответ!
И большинство взрослых дядь и тёть, кстати, не видят ошибки в рассуждениях. А вы?


Решение
А теперь давайте решим так, как, должно быть, и решал самый известный ученый XX века. Надо полагать, Альберт Эйнштейн был человеком неглупым, поэтому не стал путать понятия среднего арифметического и средней скорости. Средняя скорость находится по формуле: весь путь деленный на всё время.
Чтобы правильно решить задачу надо из времени, потраченного на весь путь, отнять время, потраченное на подъем, и разделить 1 милю на оставшееся время — это и будет средняя скорость спуска.
Сначала можно найти, сколько времени у нас есть на весь маршрут (подъем и спуск) в 2 мили. Для этого весь путь (2 мили) разделим на заданную в условии среднюю скорость на всем пути (30 миль в час), получаем 2:30=1/15 часа или 4 минуты.
Теперь посчитаем, сколько времени потратил автомобиль на подъем. 1 милю делим на 15 миль в час, получаем 1:15=1/15 часа или 4 минуты. Вот тут и становится понятен розыгрыш. Время на подъем равно времени на весь путь. Иными словами времени на спуск не остается совсем. А так как машина — это не гамма-квант, задача не имеет решения.
Макс Вертгеймер пытался одурачить своего друга Альберта Эйнштейна. История умалчивает, удалось ли ему это или нет. Если да, то, должно быть, это был единственный случай, когда один из умнейших людей на планете был одурачен. А если нет, то Альберт Эйнштейн явно повеселился и хорошо поразвлекся этой задачей. Надеюсь, что и вам она понравилась.
Источник
Уважаемые друзья! Обязательно ставьте лайки и подписывайтесь на сайт и делитесь своим мнением в комментариях!
Рекомендую также прочесть :
28 Интересных фактов про Дуэйна Джонсона https://otari.mirtesen.ru/blog/43201962727/
10 фраз, которые выдадут инфантильного человека с головой https://otari.mirtesen.ru/blog/43392294492/
«Как советская власть угробила деревню», а Сталин уничтожил миллионы крестьян России и Украины. https://otari.mirtesen.ru/blog/43083661523/
Свежие комментарии